Bányai Gábor

Matematika

A matematika szó a görög nyelvből származik, a μάθημα (máthema) szó jelentése „tudomány, tudás”, a μαθηματικός (mathematikós) pedig azt jelenti, „tudásra vágyik”.

A matematika, tárgyát és módszereit tekintve, sajátos tudomány, mely részben a többi tudomány által vizsgált, részben pedig a matematika „belső” fejlődéséből adódóan létrejött rendszereket, struktúrákat, azok absztrakt, közösen meglévő tulajdonságait vizsgálja. Régebben a mennyiség és a tér tudományaként határozták meg, a múlt század elejétől kezdve pedig a matematikáról azt tartották, hogy az a halmazelmélet absztrakt struktúráinak formális logikai szemlélettel és a javarészt erre épülő matematikai jelölésrendszerrel való vizsgálata. Ma már nemcsak az első, hanem a második álláspontot is vitathatónak, túlhaladottnak tartják egyes didaktikai szakemberek. A matematikát nehéz pontosan meghatározni, mibenlétének kérdése még manapság is, sőt manapság különösen, vita tárgya, élő és nem lezárt tudományos probléma, mellyel a matematikafilozófia foglalkozik. A matematika sajátossága elsősorban különleges témaválasztásában, kutatási területeiben és módszereiben, nyelv-és jelölésrendszerében rejlik.

Goldbach-sejtés

A Goldbach-sejtés azt mondja ki, hogy

(I.) Minden 2-nél nagyobb páros szám előáll két prímszám összegeként.

(II.) Minden 5-nél nagyobb páratlan szám előáll három prímszám összegeként.

A sejtés egyike azoknak a szélesebb körben ismert matematikai állításoknak, melyekről a szakemberek túlnyomó többsége azt gondolja, hogy minden valószínűség szerint igaz, ugyanakkor a mai napig nem rendelkezünk bizonyítással a helyességüket illetően. Christian Goldbach 1742-ben egy Euler-hez írott levelében fogalmazta meg megfigyelését, hogy minden 5-nél nagyobb páratlan szám három prímszám összege. Euler válaszul rámutatott, hogy ez ekvivalens a fenti (I.) állítással.

A több mint 250 éves problémát illetően ma is csak részeredményekkel rendelkezünk. A sejtést számítógéppel a 4·10¹⁸-nál kisebb természetes számokra^[2] igazolták. 1923-ban Hardy és Littlewood bebizonyította, hogy feltéve az általánosított Riemann-hipotézist, minden elég nagy páratlan szám három prím összege és x-ig legfeljebb 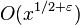páros szám nem lehet két prím összege. Az 1930-ban Snyírelman bebizonyította, hogy alkalmas s számra minden 1-nél nagyobb természetes szám s darab prímszám összege (ezt 1912-ben vetette fel Landau). Snyírelman bizonyítása teljesen elemi volt, a Brun-szitára és a Snyírelman-sűrűség általa bevezetett fogalmára épült. 1937-ben Vinogradov új módszert dolgozott ki a

összeg becslésére (itt p prímszámot jelöl) és ezt használva megmutatta, hogy a páratlan számokra vonatkozó állítás egy bizonyos korláttól kezdve igaz. Az eredeti bizonyítás nem adott konkrét korlátot. Később, ezeket a bizonyításokat effektivizálva a következő korlátok adódtak: Hardy-Littlewood -re, Vinogradov -ra és ennek javításai is 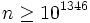-ot adnak (M.C.Liu, T.Z.Wang, 2002). J.-M.Deshouillers, G.Effinger, H. te Riele és D. Zinovjev 1997-ben az általánosított Riemann-sejtésből belátta, hogy minden 5-nél nagyobb páratlan szám három prím összege.

A honlap magyarul nem csak a weblap első oldalát jelenti, minden oldal együtt a honlap.

ÁSZF | Adatvédelmi Nyilatkozat